Скачать
西瓦定理(Ceva's theorem)的證明
Автор: 鍾笙
Загружено: 2026-02-02
Просмотров: 66
Описание:
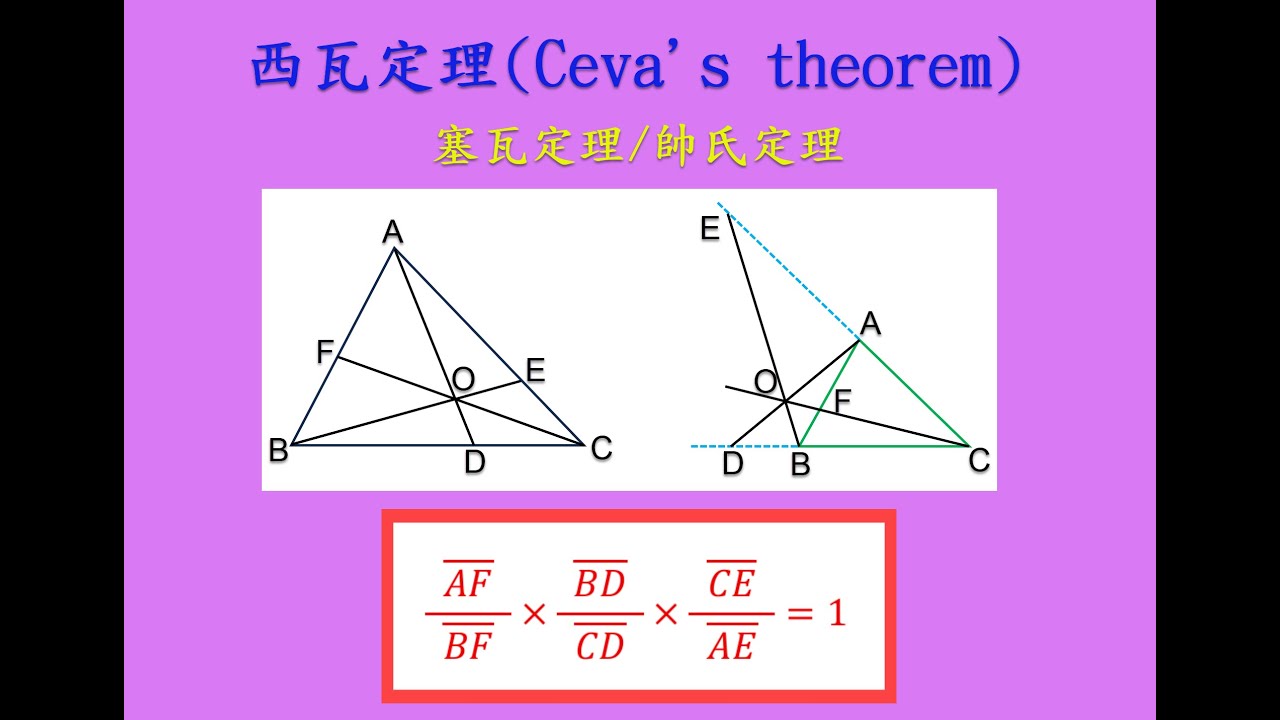
西瓦定理(Ceva's theorem)，最先由義大利數學家喬瓦尼·塞瓦證明，因而得名 ，又稱塞瓦定理或帥氏定理。西瓦線段是各頂點與其對邊或對邊延長線上的一點連接而成的直線段。
如果△ABC的西瓦線段AD線段、BE線段、CF線段通過同一點O，
則 (AF線段/BF線段)×(BD線段/CD線段)×(CE線段/AE線段)=1。
它的逆定理同樣成立：
若D、E、F分別在△ABC的邊BC線段、AC線段、AB線段或其延長線上（都在邊上或有兩點在延長線上），且滿足 (AF線段/BF線段)×(BD線段/CD線段)×(CE線段/AE線段)=1，則直線BC線段、AC線段、AB線段共點或彼此平行（於無限遠處共點）。
(與孟氏定理的等式僅在條件上有所不同，二者互為對偶定理。)
Не удается загрузить Youtube-плеер. Проверьте блокировку Youtube в вашей сети.
Повторяем попытку...
Повторяем попытку...
Доступные форматы для скачивания:
Скачать видео
-
Информация по загрузке:
