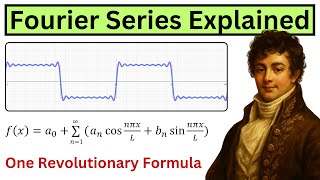
¿Qué es una Serie de Fourier?
Автор: Mates Mike
Загружено: 2023-12-06
Просмотров: 234752
Описание:
■ Para probar todo lo que ofrece Brilliant durante 30 días totalmente gratis, visita http://brilliant.org/MatesMike/ . Los primeros 200 en usar mi link obtendrán un 20% de descuento en la suscripción anual Premium de Brilliant.
■ Theorem of Bethoven: / @theoremofbeethoven , @TheoremofBeethoven
■ BLOG Juan Carlos: https://bestiariotopologico.blogspot....
■ Dibujar epiciclos: https://www.dynamicmath.xyz/fourier-e...
■ Patreon: / matesmike
■ Miembros del canal: / @matesmike
■ Instagram: @mates.mike
■ Twitter: @mike_mates
►► ALGUNOS VÍDEOS:
► SAGA DEL INFINITO: • La Paradoja del Hotel Con Infinitos Huéspedes
► SAGA DEL FACTORIAL: • ¿Qué es el Factorial en Matemáticas y para...
► LA HIPÓTESIS DE RIEMANN: • El Patrón de los Números Primos y la Hipót...
► El Orden de los Factores SÍ altera el Producto: • El Orden de los Factores SÍ altera el Prod...
► Cómo Dividir Entre 0 Sin Colapsar el Universo:
• Cómo Dividir entre 0 sin Romper el Universo
►Ecuaciones y fractales: • Cómo CREAR FRACTALES con POLINOMIOS | Mate...
Este video está patrocinado por Brilliant.
Повторяем попытку...

Доступные форматы для скачивания:
Скачать видео
-
Информация по загрузке:

![Цепи Маркова — математика предсказаний [Veritasium]](https://ricktube.ru/thumbnail/QI7oUwNrQ34/mqdefault.jpg)