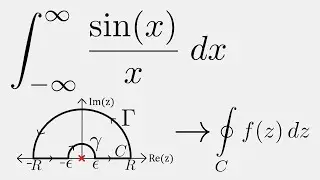The Integral That Hides Pie
Автор: Math Quest Club
Загружено: 2026-01-22
Просмотров: 339
Описание:
This integral looks impossible at first glance:
∫₀^∞ sin(x²)/x dx
The oscillations get faster and faster, the sign keeps flipping… and yet the total area converges to a shockingly clean number:
∫₀^∞ sin(x²)/x dx = π/4 (pie/4)
In this video, we show why — step by step:
• A simple substitution: u = x²
• Turning the problem into the famous Dirichlet integral: ∫₀^∞ sin(u)/u du
• A complex-analysis setup with f(z) = e^(iz)/z
• Building a contour: γ₁ and γ₃ (real axis), γ₂ (big arc), γ₄ (small arc)
• Why the big arc → 0 as R → ∞
• Why the small arc contributes a constant as ε → 0
• Extracting the imaginary part to finish the evaluation
Final result:
∫₀^∞ sin(x²)/x dx = π/4
If you like “impossible-looking” math with clean endings, subscribe for more.
#math #calculus #integrals #complexanalysis #contourintegration #dirichlet #fresnel #engineeringmath
Повторяем попытку...

Доступные форматы для скачивания:
Скачать видео
-
Информация по загрузке: