Trin Tragula General Relativity
General relativity, step by step. This is a mathematical description of the nuts-and-bolts of Einstein's general theory of relativity, with no gaps. I am concentrating on the nitty-gritty of tensor calculus including detailed derivations of tensor algebra, Christoffel symbols, and the Riemann curvature tensor. I will discuss black holes in some detail (the Schwarzschild metric), and plan to add discussion of gravitational waves and cosmology.

GRSS027 raising and lowering indices (replacement)
GRSS 158 black holes modification to flat space

GRSS 009 contravariant vector components

GRSS 189 Kruskal Szekeres part five

GRSS 133 Riemann revisited
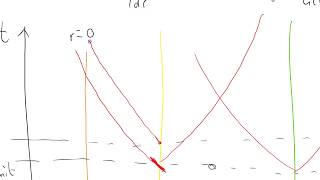
cos 22 radial light rays and cosmological redshift part one

cos 16 solutions for q using the Einstein field equations

cos 26 equation of state part one

cos 27 equation of state part two

cos 34 density deficit of the universe

cos 24 cosmological redshift using linear approximation

cos 31 Friedmann equation

cos 19 flat space might have nontrivial global topology

cos 25 Einstein field equations for a needs an equation of state

cos 10 Ricci tensor components in civilized form

cos 30 equation of state for a photon gas

cos 13 stress energy scalar

cos 18 nonstandard topological embeddings of knots

cos 21 universe with saddle like curvature solution

cos 17 closed universe has spherical geometry

cos 06 trial metric for the cosmos

cos 38 vacuum dominated universe

cos 14 Ricci tensor with one upstairs and one downstairs index

cos 29 equation of state part four interpretation

cos 03 universal time coordinate in cosmology

cos 36 radiation dominated universe

cos 09 Riemann Christoffel curvature tensor by hand

cos 37 matter dominated universe

cos 08 Ricci tensor for the trial metric

cos 32 Friedmann equation with equation of state